Magnitud de vectores

"Magnitud de vectores"
Física 1
Fátima Naveda Priego
Tercer Semestre de Bachillerato Grupo A 
Jueves 31 de Agosto del 2017 
Prof. Marco Antonio Morales Contreras 

Villahermosa, Tabasco

INTRODUCCIÓN

¿Qué es un vector?

Es una magnitud física que posee una dirección y sentido, y se representa por medio de una "flecha" en el plano.

Principalmente un vector tiene tres elementos: la dirección, el sentido, y el ángulo
Los vectores es uno de los conocimientos de las matemáticas que provienen de la física. En la  distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman magnitudes escalares aquellas en que sólo influye su tamaño. Por el contrario, se consideran magnitudes vectoriales aquellas en las que, de alguna manera, influyen la dirección y el sentido en que se aplican.

DESARROLLO

Aquí les dejo un video para que vean un ejemplo de lo que les explicaré mas adelante y se les haga mas fácil después al leer la información

Características del vector:

• Origen:Es cuando un vector es usado, parte de un punto del cual tendrá como partirá para cumplir con su objetivo clave.
• Dirección:Esta se visualiza dependiendo de la orientación que tenga en el espacio. Puede ser creciente o decreciente dependiendo de la magnitud en estudio.
• Sentido: Básicamente es hacia a donde apunta la punta de la flecha con la que es representado.
• Magnitud:aquellas propiedades que pueden medirse y expresar su resultado mediante un número y una unidad.

Hay 2 tipos de magnitudes:

• Magnitud Escalar: Cuando la magnitud es determinada por un numero (con signo) y su respectiva unidad,(distancia,rapidez,tiempo,masa,energía)
• Magnitud Vectorial: Cuando queda determinada por un número (angulo), la unidad correspondiente, la dirección y sentido,(desplazamiento,aceleración,fuerza)

Aquí se explicará como realizar operaciones con vectores:

Suma de magnitudes vectoriales

Al sumar dos vectores se obtiene otro vector (vector suma o resultante). Para obtener el vector suma es necesario recurrir a lo que se conoce como “regla del paralelogramo”. Esto es, se construye un paralelogramo que tenga los vectores como lados y se traza la diagonal del mismo para obtener el vector suma.

Si queremos sumar A + B , se dibuja uno a continuación del otro, trasladándolo. El vector resultante es el que va desde el punto inicial del primero vector hasta el final del último. Cabe destacar que la suma es conmutativa es decir:

A + B = B + A

Cuando se quiere sumar más de un vector, se procede de la misma forma anterior, pero ahora se colocan uno a continuación del otro hasta el último. Luego la recta que une el inicio del primer vector con el término del último es el vector resultante

.

Resta de magnitudes vectoriales

Para la resta se procede de la misma forma que la suma, pero el vector que resta se debe dibujar con sentido contrario, o sea el signo negativo cambia el sentido del vector. Luego el vector resultante es el que va desde el punto inicial del primer vector, hasta el final del vector que se le cambio el sentido.

Cabe mencionar que la resta no es conmutativa

Multiplicación de magnitudes vectoriales

Multiplicación por un número positivo mayor que 1:

En este caso el vector que se multiplica aumenta de modulo según el valor del escalar que multiplica y su dirección y sentido nunca cambian.

Ejemplo: sea el vector A= (3,2) el cual se multiplica por 2, entonces tenemos de forma algebraica: 2 (3,2)= (6,-4)

Multiplicación por un número positivo menor que 1 y mayor que cero:

En este caso el escalar que  multiplica al vector, hace que el modulo disminuya en cierto valor manteniendo su dirección y sentido.

Ejemplo: sea el vector B= (4,2) si lo multiplicamos por 0,5 entonces tenemos de forma algebraica:

0,5 (4,2)= (2,1)

Multiplicación por un -1:

En este caso al multiplicar un vector por escalar -1, o cualquier numero negativo cambia el sentido del vector y si es un número mayor o menor que 1 cambia el tamaño del módulo también.

Ejemplo: Sea C= (4,2) y se multiplica por -1, entonces tenemos que: -1 (4,2)= (-4,2)

División de magnitudes vectoriales

No puede definirse tal división vectorial. Si a y b son dos vectores dados,

la ecuación

a x v = b

tiene infinitas soluciones v. Solo es necesario que a y v esten en un plano

perpendicular a b, y que el paralelogramo determinado por a y v tenga área

|b|, lo que puede conseguirse de un infinito (continuo) de formas, variando

el ángulo que froman a y v, y el módulo de v.

Por tanto, no podemos 'dividir' por el vector a. Es decir, el producto
vectorial, entre otras, no tiene la propiedad de elemento inverso.

Si un vector se multiplica por un escalar positivo, su magnitud se incrementa en esa cantidad. Cuando se multiplica por un escalar negativo también cambiará el sentido de la dirección del vector. En la figura 2-2 se muestran ejemplos gráficos de estas operaciones.

Producto de un escalar por un vector

El producto de un escalar por un vector da por resultado otro vector, con la misma dirección que el primero. Al hacer la multiplicación, el escalar cambia el módulo del vector (gráficamente el largo) y en caso de ser negativo cambia también el sentido. La dirección del vector resultado es siempre la misma que la del vector original.

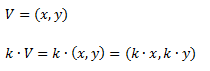
Matemáticamente se realiza multiplicando al escalar por cada una de las componentes del vector.

Si por ejemplo el vector V tiene 2 coordenadas:

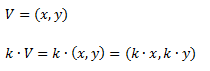
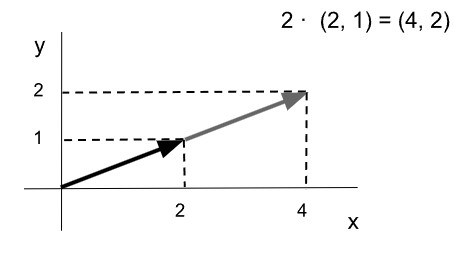
Ejemplo

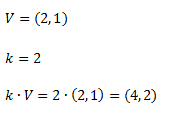
CONCLUSIÓN

Se pueden relacionar los vectores a la vida diaria en casi todo.Además de aprender diversos métodos de resolución de los mismos

Por ejemplo, cuando caminamos, describimos sumas de vectores en los que los vectores son sumas de distancias con cierta dirección y sentido, al andar en un automóvil, las distintas velocidades a las que andamos son distintos vectores. A fin de cuentas, cualquier cosa a la cual le puedas asignar un número o una magnitud y a la vez asignarle una dirección (y un sentido) es un vector.
Con este trabajo se busca desarrollar los siguientes atributos de las competencias genéricas:
1.- Expresa ideas y conceptos mediante representaciones linguísticas, matemáticas y gráficas
2.- Sigue instrucciones y procedimientos de manera reflexiva, comprendiendo como cada uno de sus pasos contribuyen al acance de un objetivo.
3.-Utiliza las tecnologías de la información y comunicación para procesar e interpretar información.

Aquí por ultimo les dejaré un ejemplo de como realicé el tema de los vectores en Geogebra, en la parte izquierda encontrarán los datos de las medidas de los vectores, angulos, etc. espero les sirva este ejemplo para reforzarse.

Referencias Bibliográficas

Profesorenlinea.com.mx. (2017). Distancia entre dos puntos. [online] Available at: http://www.profesorenlinea.com.mx/geometria/Distancia_entre_dos_puntos.html [Accessed 28 Aug. 2017].

(Fernández, perfil and Fernández, 2017)

Robles, F. (2017). ¿Cuáles son los 3 Elementos de un Vector? - Lifeder. [online] Lifeder. Available at: https://www.lifeder.com/elementos-vector/ [Accessed 30 Aug. 2017].

Anon, (2017). [online] Available at: http://ocw.unican.es/ensenanzas-tecnicas/fundamentos-fisicos-de-la-ingenieria/material-de-clase-2/Escalares_y_vectores.pdf [Accessed 30 Aug. 2017].

Física de nivel básico, nada complejo.. (2017). Vectores. [online] Available at: https://www.fisic.ch/contenidos/elementos-b%C3%A1sicos-1/vectores/ [Accessed 30 Aug. 2017].

Definista (2017). ¿Qué es Vector? - Su Definición, Concepto y Significado. [online] Conceptodefinicion.de. Available at: http://conceptodefinicion.de/vector/ [Accessed 30 Aug. 2017].